日本瑞穗信息综研株式会社 社会技术室
徐 敏, 小林敬幸, 眞鍋 尚
Min XU, Hiroyuki KOBAYASHI, Takashi MANABE
论文概要
本论文主要介绍以盾构衬砌横断面为对象,利用可以考虑错缝拼装效果的梁—弹簧模型,通过位移响应法进行抗震数值解析。以双圆盾构结构为例,在地基弹簧模型下预先设置地震时地基发生的位移值,将周边地基产生的剪力直接作用在结构上进行抗震数值分析。这种数值解析方法和FEM振动解析法所得到的结果比较,对地震时所产生的内力进行论述和分析。
Key Words: seismic analysis, seismic deformation, M-K method, dynamic analysis
前言
地震发生时与地上建筑物比较地下建筑物的损坏要小的多,这一观点已经被普遍认识。但是,1995年1月17日日本兵库县南部发生大地震时地下隧道的一部分却遭受了破坏。另外2004年10月23日日本中越地区发生地震时,不受大变形影响的抗震性能很高的地下隧道也同样发生了破损现象。新干线鱼沼线、上越线和南津线等线路内的压缩部位的管片衬砌都有破坏现象,所以为了确保地下建筑物的抗震性能而进行抗震数值解析是十分必要的。
关于地下结构的抗震性能,目前为止大致分为静力学和动力学的数值解析方法。其中位移响应法作为一种简便的计算方法被应用于地下结构的数值解析中。
在日本,盾构隧道的设计方法中梁—弹簧模型被普遍采用。它是以管片作为梁单元、管片间的接头以弹簧模型化用转动刚度作为参数、管片环间的接头以弹簧模型化用径向刚度作为参数、衬砌与地基间以地基弹簧模型化用地基反力刚度作为参数的梁—弹簧结构模型来进行计算解析的方法。综上所述梁—弹簧模型可以体现出盾构衬砌的管片接头、环间接头和错缝拼接效果的特性,是一种合理的数值解析方法。
以盾构隧道的抗震性能分析为目的,利用梁—弹簧模型采用位移响应法将是一种简便的计算分析方法。为了检验这种基于梁—弹簧模型的位移响应法(以下简称为2D-M-K法),利用最为常用和精确的三次元振动解析法(以下简称3D-FEMD法)进行比较和分析。
本解析就是以双圆盾构隧道为例,对2D-M-K法和3D-FEMD法的抗震计算解析结果进行比较。
解析方法和条件
在盾构隧道横向的抗震解析方法中,最常用的有位移响应法和振动解析法。位移响应法是地震发生时在结构横断面上所产生的内力按照静力学的分析法进行解析的一种方法。振动解析法是把隧道结构和地基一体化,加入地震发生时的加速度,随着时间的变化计算出结构应力的一种方法。
一般来说位移响应法有以下步骤:(1)地震振动力的设定→(2)地基振动响应解析→(3)地震时产生的外力计算→(4)隧道·地基的结构体系解析。振动解析法有以下步骤:(1)地震振动力的设定→(2)振动解析。本论文使用的2D-M-K法和3D-FEMD法的解析步骤如表1所示
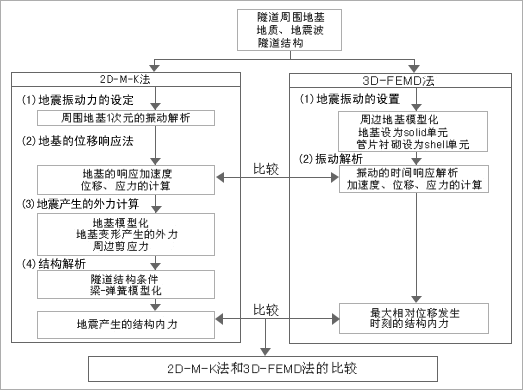
表1 解析步骤
2.1 解析条件
2.1.1 地震波
本解析使用的地震波如图2所示的1995年日本兵库县南部所发生的强震记录数据。
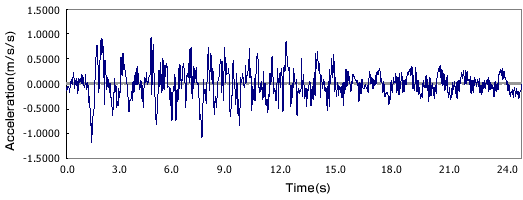
図2 地震波图
2.1.2 地基和隧道结构特性
本解析使用的地基特性如图3和表2所示。隧道结构如图4~8所示,在地面下GL-14.0m处建设的内径2.85m,外径3.15m的双圆盾构结构。结构的各个特征值如表3、4所示。
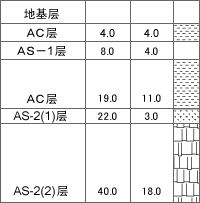
図3 地基分布图
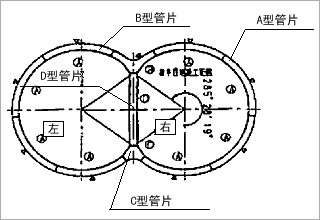
図4 衬砌结构图

図5 A型管片
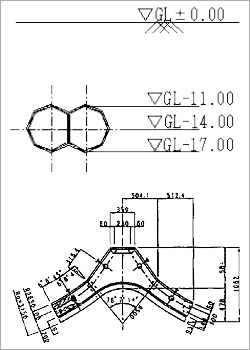
図6 B型管片
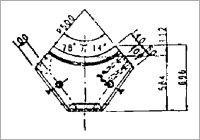
図7 C型管片
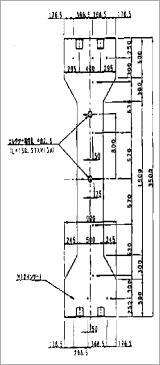
図8 D型管片图
You can scroll left and right with your finger to view the table contents.
| 地基 | 层厚 (m) |
密度 γ(KN/m³) |
剪切刚度G (KN/m²) |
泊松比 ν |
|
|---|---|---|---|---|---|
|
填土 |
AC |
4 |
14 |
11181 |
0.497 |
|
砂土 |
AS-1 |
4 |
19 |
7933 |
0.497 |
|
粉土 |
AC |
11 |
17 |
8672 |
0.496 |
|
砂土 |
AS-2(1) |
3 |
20 |
5940 |
0.482 |
|
砂土 |
AS-2(2) |
18 |
20 |
79420 |
0.482 |
表2 地基特征值
You can scroll left and right with your finger to view the table contents.
| 弹性刚度(KN/m²) |
3.9X107 |
|---|---|
| 管片宽度(m) |
1 |
| 管片厚度(m) |
0.3 |
| 截面面积(m²) |
0.3 |
| 惯性矩(m4) |
0.00225 |
| 单位长重量(KN/m) |
7.8 |
| 泊松比ν |
0.2 |
表3 管片特征值
You can scroll left and right with your finger to view the table contents.
| 管片接头转动刚度(KN·m/rad) |
正弯矩 |
负弯矩 |
|---|---|---|
|
6.00E+04 |
4.00E+04 |
|
| 环间接头剪切刚度(KN/m) |
轴方向 |
径方向 |
|
5.00E+05 |
5.00E+05 |
|
| 地基反力刚度系数(KN/m³) |
切线方向 |
法线方向 |
|
2.90E+03 |
8.60E+03 |
表4 弹簧刚度
2.2 解析方法
2.2.1 2D-MK法
对使用的地震波进行加速度计算,将振动波作用在地基1次元模型上进行振动解析。使用‘SHAKE’解析软件得出地基GL±0.00~GL-40m间的相对位移和剪切应力。作为地震时产生的外力,管片衬砌的惯性力忽略不记,随着时间的变化产生的地基位移中变化最大时刻的位移和周边剪力作用于解析模型上。
对于隧道结构的解析则采用在日本盾构设计最为常用的结构模型梁-弹簧的3环模型。如图9所示,管片接头以转动弹簧为模型,刚度参数的计算按照村上·小泉2)(M-K法)的方法求出,环间接头则以剪切弹簧为模型,管片衬砌周边的地基以地基弹簧为模型,地震时的地基反力参数的计算方法是把1次元地基模型的振动解析所得的低减刚度值代入公式(1)中求出,切线方向是法线方向的1/3。
You can scroll left and right with your finger to view the table contents.
|
Kr=3E/(1+ν)(5-6ν)R |
(1) |
|
Ks=1/3Kr |
(2) |
You can scroll left and right with your finger to view the table contents.
|
Kr |
法线方向的地基反力系数(KN/m³) |
|
Ks |
切线方向的地基反力系数(KN/m³) |
|
E |
地基的变形系数(E=2(1+ν)G)(KN/m²) |
|
G |
地震时的低减刚度值(KN/m²) |
|
R |
管片衬砌的半径(m) |
|
ν |
泊松比 |
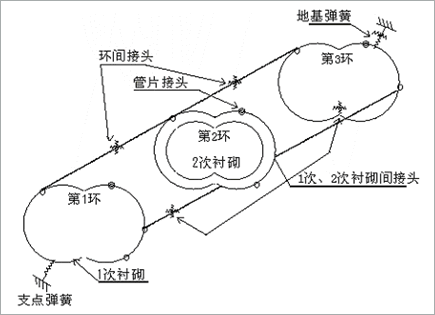
図9 梁-弹簧模型图
地震引起的结构位移以地基弹簧位移的形式表现,周边剪切力则直接作用在管片衬砌的梁单元上,分为法线方向、切线方向的分布荷载作用,计算出地震时的内力。使用的解析软件为『Moleman』。
2.1.2 3D-FEMD法
3D-FEMD法是把管片以壳单元要素为模型,环间接头和管片接头以梁要素为模型,在结构?地基一体化的解析对象上直接作用振动力来进行动力计算的方法。3次元构造模型如图10所示。

図10 构造模型图
本解析是以2环为解析对象,沿地基方向1m+1m的幅宽面(solid要素)为模型。解析对象范围是地表以下垂直方向40m深,隧道双圆圆心左右各150m宽。模型示意如图11所示。

図11 3D-FEMD模型图
解析结果和分析
3.1 解析结果
上述方法进行解析得到的结果如下所示。3D-FEMD法计算所得的随着时间变化上下端的相对位移如图12所示。从图中得出最大位移发生时刻为2.3s。 SHAKE和3D-FEMD法计算出的最大相对位移如图13所示。2D-M-K法和3D-FEMD法的解析结果,位移图如图14所示、内力图如图15所示。
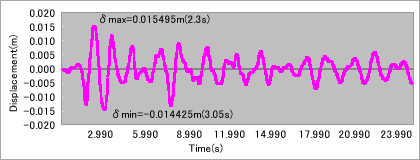
図12 隧道上下端随时间变化的相对位移
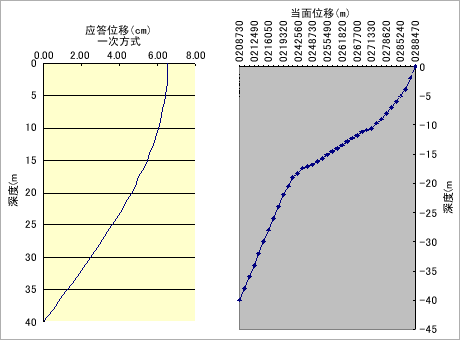
図13 地震最大位移图
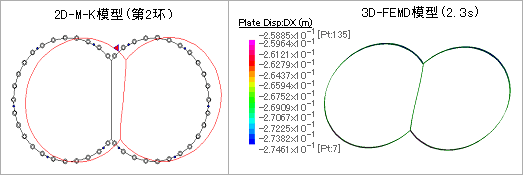
図14 地震发生的位移图
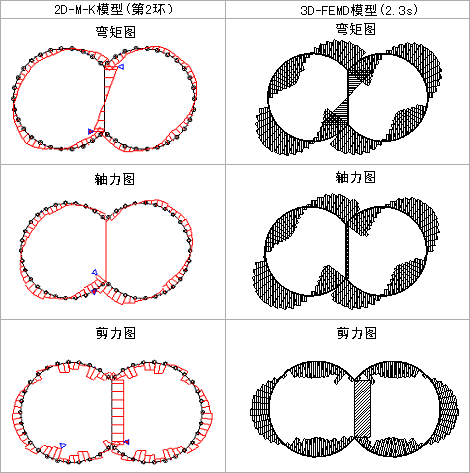
図15 地震时的管片内力图
3.2 解析结果的分析
由3.1节所示的解析结果,对管片主体上地震产生的内力进行分析。首先对图4~8所示的管片各个内力值进行比较,如表5所示。
You can scroll left and right with your finger to view the table contents.
| A型管片 | 2D-M-K法(第2环) | 3D-FEMD法(2.3s) | |
|---|---|---|---|
| 弯矩(KN·m) |
+Mmax |
177.41(0.98) |
179.91 |
|
位置 |
[1] |
[1] |
|
|
-Mmax |
-188.12(1.04) |
-179.90 |
|
|
位置 |
[2] |
[2] |
|
| 轴力(KN) |
+Nmax |
151.32(1.03) |
147.32 |
|
位置 |
[3] |
[3] |
|
|
-Mmax |
-133.97(0.96) |
-139.25 |
|
|
位置 |
[4] |
[4] |
|
| 剪力(KN) |
MAX |
100.88(0.89) |
113.16 |
|
位置 |
[5]、[6] |
[5]、[6] |
|
| B型管片 | 2D-M-K法(第2环) | 3D-FEMD法(2.3s) | |
| 弯矩(KN·m) |
MAX |
170.45(0.99) |
171.7 |
|
位置 |
[7] |
[7] |
|
| 轴力(KN) |
MAX |
156.42(1.00) |
156.38 |
|
位置 |
[8] |
[8] |
|
| 剪力(KN) |
MAX |
126.99(1.28) |
99.01 |
|
位置 |
[9]、[10] |
[9]、[10] |
|
| C型管片 | 2D-M-K法(第2环) | 3D-FEMD法(2.3s) | |
| 弯矩(KN·m) |
MAX |
141.92(0.79) |
179.9 |
|
位置 |
[11] |
[11] |
|
| 轴力(KN) |
MAX |
184.10(1.15) |
160.47 |
|
位置 |
[11] |
[11] |
|
| 剪力(KN) |
MAX |
82.37(1.45) |
56.86 |
|
位置 |
[12]、[13] |
[12]、[13] |
|
| D型管片 | 2D-M-K法(第2环) | 3D-FEMD法(2.3s) | |
| 弯矩(KN·m) |
+Mmax |
241.32(0.84) |
288.47 |
|
-Mmax |
-297.70(0.85) |
-351.72 |
|
| 轴力(KN) |
MAX |
-2.729(1.80) |
-1.52 |
| 剪力(KN) |
MAX |
139.15(0.69) |
202.10 |
( )内的数字是対3D-FEMD法(2.3s)结果的比例
表5 解析结果的比较
由图14、15两种方法的结果比较分析,结构的变形模型、地震产生的内力分布模型大体一致。参考图16、表5,A型管片的地震产生的内力中正弯矩、负弯矩和轴力的最大值大体上相同。2D-M-K法算出的剪力的最大值大约减小10%左右。
对管片和立柱连接的特殊部位的结果进一步观察,可以得到两种方法下B、C型管片的内力结果有一定的差别。对于产生这一结果的原因进行分析,2D-M-K法的地基位移是利用1次元地基模型计算的,所以同一个深度的结构部位的位移是相同的,而3D-FEMD法的地基位移是利用3次元地基模型计算的,所以同一深度的结构部位的位移随着水平方向位置的不同而不同。对两种方法得到的位移值进行比较,图16[6]~[14]的区间内位移比如图17所示。对图17进行分析可以得出两种方法计算出的位移在管片和立柱连接的特殊部位具有差别这一结论,这也正是两种方法得到的内力具有差别的原因。另外,受这一原因的影响,立柱部分计算出的结果也有所差别。2D-M-K法是基于梁-弹簧模型基础之上,利用最为简便的振动解析法1次元地基模型计算出地基位移,那么在保留这一简便方法的同时就要对地基的特征值进行调整来达到和3次元地基模型计算出的位移相同的目的。经过以上的分析,可以得出在双圆盾构结构建立梁-弹簧计算模型时,对于一些特殊部位的地基弹簧要进一步调整的结论。
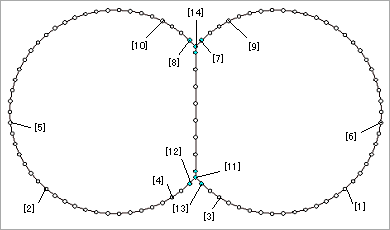
図16 表5所示的内力位置图
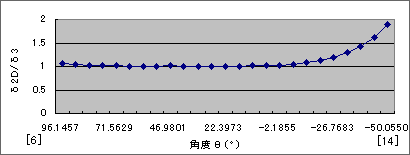
结束语
本论文介绍了基于梁-弹簧模型的盾构衬砌结构的横向抗震数值解析,利用位移响应法对双圆盾构结构地震时产生的地基变形进行处理,地基弹簧预先设置位移、周边剪力直接作用在结构上,进行抗震数值解析。这种方法和3次元FEM法的振动解析结果进行比较,对管片在地震时产生的内力进行了分析。
由分析结果得到,双圆盾构结构除了某些特殊部位外两种方法解析结果大体上是相同的,特殊部位存在一定差别,对产生的差别进行分析并找出原因。最后,在双圆盾构结构建立梁-弹簧计算模型时,对于一些特殊部位的地基弹簧要进一步调整。
参考文献
- 1)土木学会编辑:平成16年新泻县中越地震第一次调查团调查速报,(2005年)
http://shake.iis.u-tokyo.ac.jp/chuetsu/ - 2)村上博智,小泉淳:关于被密封的被分割的圆环的抵抗装载机制:土木学会论文报告集 No.727,(1978年)
- 3)川岛一彦:地下构造物的耐震设计 鹿岛出版会,(1995年)
- 4)土木学会编辑:开凿隧道的耐震设计 隧道·程序库9 丸善株式会社
询问
担当:社会技术室