石油・天然ガス堆積盆評価システム SigmaBasin（シグマベースン） 原理 地質シミュレーションモデル

一覧に戻る

1地質の埋没・圧密の再現

堆積盆の進化の過程で、根源岩、キャリアベッド、貯留岩、キャップロックを含む各地層がどのような位置関係にあるのか、つまり、ある時代にどの程度各地層が埋没するのかは、油・ガスの生成・移動を再現する上で重要な問題である。本来は基盤の沈降や地層の変形により堆積場が生じ、そこに堆積物が供給され堆積盆は進化するが、その結果ある時代にその部分で堆積速度が速く堆積物が厚く堆積する。そしてその下の地層にとっては埋没速度が速いという現象として現れる。したがって各地層の埋没は、その上に新しく堆積した堆積物の層厚分だけ深度を深めることにより再現できるが、ここで注意しなければならないのは地層の「圧密」である。

地層は埋没していくに従い徐々にその厚さを減じ、堆積盆の深部では堆積直後の半分以下になってしまう。

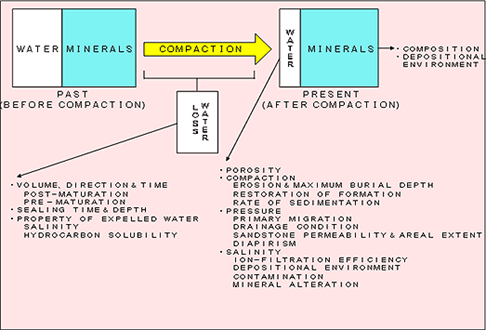
圧密の概念

この圧密現象は、堆積直後の堆積物に40〜80%程度含まれている海水等の流体が、その上に次々に堆積する新しい堆積物の荷重により排出されることにより生じる。地層の埋没を再現する時には、各地層の深度を深めることに加え、この地層自身の層厚現象も圧密補正により再現する必要がある。

地層中に含まれている水は、堆積物中の固体粒子の間隙に存在しており、その割合つまり「孔隙率」は圧密の進行とともに減少する。「孔隙率の減少」は坑井等で良く観察されている現象であり、深度の増加とともに指数関数的に減少することが知られているが、堆積盆によりその減少の仕方に多様性がある。その理由としてまず挙げられるのが岩相の多様性である。

荷重が増加すれば、力学的により安定な状態に堆積物中の固体粒子が配列を変えたり、粒子自体がつぶれたり砕けたりすることにより孔隙率が減少するが、その様子は固体粒子を構成する物質の力学的な性質により異なってくる。また、次々に堆積する堆積物により荷重が増加しても、地層中に含まれる水が排出されない限り、孔隙率の減少や圧密は進行しない。つまり圧密は水等の流体移動と密接な関係があり、岩石中を流体が流れる時の流れやすさである「浸透率」も岩相によって異なるため、孔隙率の減少の仕方が異なるのである。例えば浸透率は細粒な泥岩の方が小さいため、新たな荷重が加わっても短時間に水の排出が完了しない。そこで流体を排出させ孔隙率を減少させることで解消される荷重増加、つまり圧力の増加が、流体の圧力増加として残ってしまい「異常高圧層」を形成する。

既存のソフトウエアでは、孔隙率の減少を荷重つまり圧力のみの関数として与えているものがほとんどである。さらにその減少は、堆積物中の固体粒子の配列変化や粒子自体の変形・破壊により起ると考えられているため、特に固体粒子に架かる荷重である「有効応力（σ）」の関数として与えており、有効応力が大きくなれば孔隙率の減少が進行するとしている。有効応力は、荷重の総計と荷重（S）＝有効応力（σ）＋間隙水圧（P）という関係で結ばれている。堆積物の密度から計算した荷重（S）と流体移動を再現した結果得られる間隙水圧（P）の差が、有効応力（σ）に相当し、その増加により孔隙率減少を再現している。この有効応力増加と孔隙率減少との関数形の違いが、各ソフトウエアの特徴となっており、

既存ソフトウエアにおける孔隙率減少を表現する数式

その関数の定数を変えることにより、岩相の違いを表現できる。このモデルでは、もし異常高圧層が形成されれば、上の式における間隙水圧（P）が大きくなるため、有効応力（σ）が小さくなり孔隙率の減少が妨げられる。そして間隙水圧が十分に大きくなると水の排出量が増え、その結果異常高圧が解消されていくが、この過程では間隙水圧が減少し有効応力が増加するため、孔隙率の減少が再び進行することになり、実際に観察される事実を再現することが可能なのである。

孔隙率は、「圧密」のみならず、油・ガス移動の「通路」として、あるいは油・ガスを貯める「器」として重要であるが、その減少を厳密に言えば、圧力による「物理的なプロセス」のみならず、「化学的なプロセス」によっても進行する。多くの化学的プロセスは温度変化に支配されており、そのため堆積盆の熱史が異なれば化学的なプロセスによる効果の程度が異なってくる。従ってこのことも孔隙率減少の多様性の一因となっている。当研究室（石油公団石油開発技術センター地質・地化学研究室）では、圧力に支配された、

1. (1)再配列（repacking）
2. (2)破壊（Crushing）
3. (3)流動変形（Ductile Flow）

という物理的プロセスのみならず温度や時間にも支配されている、

1. (4)圧力溶解（Pressure Solution）
2. (5)圧力溶解物の沈殿（Welding）
3. (6)鉱物変質（Clay Diagenesis）
4. (7)セメンテーション（Cementation）

による孔隙率減少のモデル化にも取り組んでいる（Waples and Kamata,1991）。

モデル構築の方法としては、まず上の7つのプロセスをそれぞれ物理化学的に表現し、数式化する。例えば（4）圧力溶解は「拡散（Diffusion）」によって、（6）鉱物変質は「反応速度論（Kinetics）」によって、（7）セメンテーションは「セメント物質（Silica,Calcite）の溶解度」、「流入してくる流体の流量」、「流入流体中のセメント物質の濃度」の関数として数式化する。次に各岩相の孔隙率減少をその7つのプロセス内の幾つかの組み合わせで表現する。

そして各岩相において、このモデルによるシミュレーション結果と実際の坑井試料において観察される孔隙率の実測値との比較を行い、表現した数式、特に定数を補正するという試行錯誤を繰り返しモデルの構築を行っている。

孔隙率減少を圧力（荷重）のみの関数とした従来のモデルでは、計算値と実測値が余り合っていないが、化学的なプロセスをも考慮したモデルでは良い一致を見ている。

2流体移動の再現

1.で触れたように、地層の圧密はそこに含まれる水が排出（移動）されて初めて進行する。逆に異常高圧層は流体の排出が十分に行われないと形成される。また化学的なプロセスによる孔隙率減少（つまり続成作用）の幾つかは、移動する流体が運搬する物質により影響を受ける。さらに移動する流体は熱も運ぶため、生成現象を支配する熱構造や熱史に対しても影響を与える。もちろん生成した油・ガスの移動も、流体移動のひとつである。このように「流体移動」は様々な地質現象に影響を与えるが、油・ガスの移動は、通常の水の移動に油・ガスが加わった2相あるいは3相流での移動を指しており、特殊な場合と考えられる。まずここでは「水」という1相の移動を前提として話を進めたい。

流体の移動は、「ダルシーの法則」に従うことが知られている。

流体移動を表現する数式（ダルシーの法則）

この法則はDarcyによって経験的に見出され、その後Hubbertによりその物理的な解釈がなされている（Bethke,1989）。つまり、任意の方向の流体の流量（ql:cm³／cm²・sec）は、流れる2地点の「流体ポテンシャル（Φ）」の差に比例し、その比例定数を流体が移動する物質の「浸透率（k:cm²,d）」を移動する流体の「粘性（μ:g／cm・sec,cp）」で割った「透水係数」とする法則である。通常ポテンシャル（Φ）の差は「営力」と呼ばれ、（1）2地点における「流体の圧力」、（2）2地点の「標高」の差の合計として表現される。図では（1）圧力差が「dP／dl」、（2）標高差が「dz／dl」で表されており、2地点における流体の圧力差が大きいほど、また標高差が大きいほど流体は多く流れるのである。

図上の式はある方向、つまり1次元での流体移動を表現したものであるが、実際の堆積盆では流体は2次元あるいは3次元方向に移動する。そこで流体移動を再現するためには、堆積盆のある地点における流体の「流入」と「流出」を全ての方向について計算しなくてはならない。しかし逆に堆積盆のある部分にとって見れば、そこに貯めておくことができる物質量（質量）は決まっており一定である。従ってそこに収まり切らなかった物質は、さらに隣接する部分に移動して行かねばならなくなる（最終的には地表へ排出される）。このような堆積盆の各地点における「質量保存」現象を計算することにより、堆積盆全体の流体移動を再現することができる。またこの一連の計算を各時間において行えば、流体移動の歴史を知ることも可能である。

ここで注意しなくてはならないのは、

• 移動した流体を留める「器」である孔隙率が、埋没（圧密）とともに変化すること。
• 流体自体は温度上昇に伴い膨脹する。
• 実際の流体は圧力上昇に伴い圧縮される。

という点である。

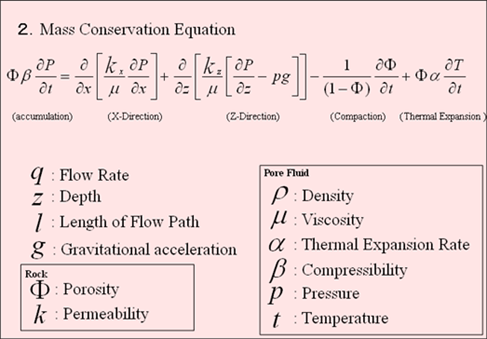
流体移動を表現する数式（質量保存式）

そこで 流体移動を表現する数式（質量保存式）の最終的な2次元での「質量保存式」では、これらのことを考慮している。このような流体移動の様子を模式的に示したのが下図である。

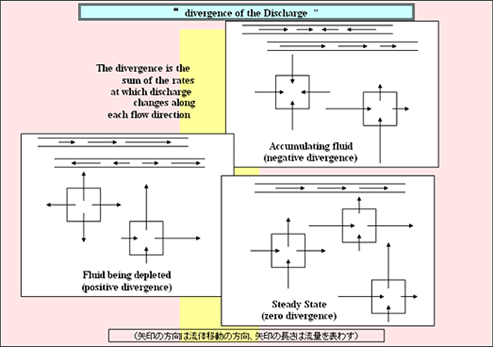
堆積盆における流体移動の3つのタイプ

ある地点において様々な方向から流れ込んでくる流体の総量と流出していく流体の総量が等しいならば、その地点では見かけ上何事も起っていないように見える（Steady State）。しかし圧密が起っていれば、孔隙率の減少量に相当する流体が、そこから流失（Being Depleted）することになり、流出量が流入量を上回る。逆に流入量が流出量を上回れば、流入量から流出量を差し引いた流体が集積（Accumulating）することになる。

3フラクチャリングの再現

流体移動に最も影響を及ぼす物性値は岩石の「浸透率」であるが、構造運動に伴う「フラクチャリング」はこの浸透率を変化させると考えられる。そこで当研究室では、この「フラクチャー浸透率」のモデル化にも取り組んでいる（Larson et al.,1991）。このモデルではフラクチャーは、地層の受ける「歪み（Strain）」の大きさが地層の「歪みに対する抵抗力（延性：Ductility）」を越えるとき（つまり「歪み＞延性」の時）生じると仮定している。

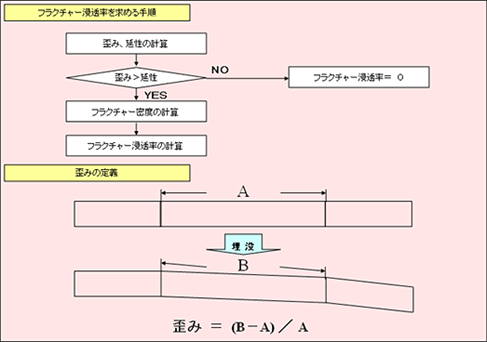
フラクチャリングをシミュレーションする手順と歪みの定義

実際の計算では、まず地層の受ける歪みと地層の延性を計算する（図上）。歪みは地層が埋没する際に受ける伸縮作用により生じるとし、簡便的に 図下のように計算する。地層の延性は、破壊直前の最大歪みのことである、岩相、孔隙率、圧力（荷重）、温度等によって変化すると考えられるが、 各岩相に対し深度の関数として与える。

フラクチャリングが起った時には、「歪み-延性」をフラクチャリングの総量（あるいは総延長）として、その浸透率の計算を行うが、それに先立ちフラクチャー密度（本数）の計算を行う。フラクチャー密度は、その総量を1本の開口幅（Aperture）で割れば求められるが、実際のフラクチャーは必ずしも伸縮方向に対して垂直に入るわけではないため、1本の開口幅（b）をその方向（θ）により伸縮方向の変位量に補正し計算する。開口幅や方向はデフォルト値として与えられないが、ユーザによって指定することも可能である。
全てのフラクチャーによる浸透率は、上で求めた密度（本数）と、
k ix＝cos2（θ）・b2／12（水平方向）
k iz＝sin2（θ）・b2／12（垂直方向）
という1本のフラクチャーの浸透率により計算する。

4熱史の再現

堆積盆の熱史を知ることは、堆積盆評価を行う上で極めて重要である。なぜならば、石油生成反応を含めて大部分の化学反応は、温度に依存しているからである。従って、もし温度構造あるいはその歴史を正確に再現しなければ、石油生成・移動をシミュレーションする段階で誤差がさらに増幅され、精度良いシミュレーションができなくなる。

現在の地球の熱構造は、地球の進化の結果、地下深部で温度が高く、地表付近で温度が低くなっている。そこでその熱の不均衡を解消するために、地下深部から地表付近に向って熱が発散されている。特にそれが顕著な所は、火山や中央海嶺となっている（水谷他、1980年）。

堆積盆の温度構造およびその歴史は、この発散する熱がどのように堆積盆中を移動するかによって支配されている。熱エネルギーは主に、

1. (1)伝導（Conduction）
2. (2)対流（Convection）

という2つのメカニズムによって移動する（Welte and Yukler,1981;Lerche,1989）。また、この他、岩石中に含まれる「放射線源（Radio active Source）」も、自ら崩壊し熱エネルギーを発生するが、堆積物中にそのような元素が大量に含まれていることは少なく無視して構わない。

伝導（Conduction）は、重力や圧力による移動と同様なポテンシャル・フローのひとつであり、温度（ポテンシャル）が等しくなるように、温度（ポテンシャル）が高い所から、温度（ポテンシャル）が低い所へ、熱（エネルギー）が流れる。分子レベルで考えれば、温度上昇に伴うエネルギーの増加が、物質を構成している分子の振動や回転などの運動を活発化させることから、伝導とは活発化したある分子の運動（エネルギー）が、分子間の結合を介して、他の分子に伝わっていくことであると解釈できる。

この伝導の概念を数式化したのが下図である。

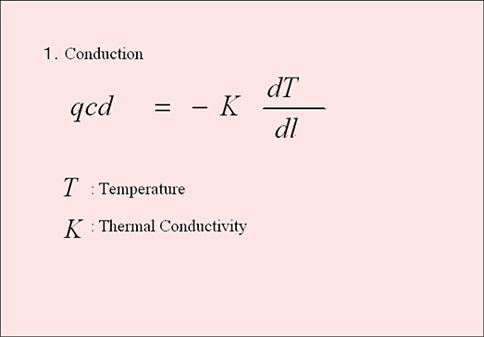
熱移動を表現する数式（伝導）

熱流量（q cd:cal／cm²・sec）は、熱が伝わる2点間の温度差（dT／dl:温度勾配）に比例し、その比例定数（K）を「熱伝導度（Thermal Conductivity:cal／cm²・sec・℃）」という（Cao and Lerche,1987;Ungerer,et al.,1984年）。熱伝導度は、熱の伝え易さを示す物質（岩石）固有の物性値である。つまり基盤から伝わってくる熱量が一定である場合、熱伝導度が大きいほど熱は速く伝わり、その結果温度差が小さくなる。逆に熱伝導度が小さいほど熱は遅く伝わり、温度差が大きくなる。

一般に堆積物の熱伝導度は、堆積物を構成する物質、つまり孔隙中に存在する流体やマトリックス中の鉱物の熱伝導度によって表されており、それらが堆積物中に占める割合の乗数となっている。砂岩を構成する石英の熱伝導度は高く、水や泥岩を構成する粘土鉱物の熱伝導度は低いため、岩相の変化や孔隙率の変化に伴い堆積物（全岩石）の熱伝導度は変化する。従って基盤から伝わってくる熱量が一定でも、岩相や孔隙率減少の仕方により、堆積盆あるいは一つの堆積盆各所でも地温勾配が異なってくる。

この基盤から伝導してくる熱量は、地表温度と同様に熱史を計算する時の「境界条件」であり、「地殻熱流量（Heat Flow）」と呼ばれている。その単位はcal／cm²・secあるいはW／m²である。つまり単位面積当たり単位時間に伝わってくる熱量のことであり、地殻熱流量が大きければ基盤から伝わってくる熱量は大きくなるが、地温勾配あるいは基盤での温度が高くなるわけではない。
堆積盆中を移動する流体は、温度つまり熱ポテンシャルを持っている。従って流体が移動することにより、それに乗って熱が運ばれる。つまり水等の流体が、圧力等の営力によって堆積盆の深部から表層へ素早く移動すれば、深部で高温化している水の熱により低温の表層が暖められるという現象がおきる。これを対流（Convection）と呼んでいる。

対流による熱流量（q cv:cal／cm²・sec）は、「流体移動量（V:cm³／cm²・sec）」と「移動前後の温度差（dT／dl）」と移動流体を単位体積当たり温度を1℃上昇させるために必要な熱量」の積によって表現される。「単位体積当たり1℃上昇させるために必要な熱量」は、高温から低温に移動する場合には、温度を1℃降下させる時に放出される熱量に相当し、単位「質量」あたり温度を1℃上昇させるのに必要な熱量である「熱容量（Heat Capacity,C pw:cal／g・℃）」と移動流体の「密度（ρ:g／cm³）」の積で表現される（下図）。

熱移動を表現する数式（対流）

実際の堆積盆では熱も流体と同様に、2次元あるいは3次元方向に移動する。そこで堆積盆のある地点における温度は、その地点における「伝導」と「対流」による熱の「流入」と「流出」を全ての方向について計算し、その結果残った熱量によって決定される（下図）。

熱移動を表現する数式（熱量保存式）

上図は、「垂直方向（Z）」と「水平方向（X）」の2次元の「熱量保存式」であり、左辺が移動の結果残った熱量を表し、右辺は左辺の熱の集積により決定される温度変化を計算している。つまり計算する地点の温度変化は左辺により計算される熱の集積量をその地点の熱容量で割れば求められるのである。この熱量保存式による計算を堆積盆の全ての地点において行えば堆積盆の「温度構造」が、さらに全ての時間について行えば、堆積盆の「熱史」を再現することができる。

出典：石油公団 地質・地化学研究室
「堆積盆評価システム」の概要－大型研究『原油・根源岩対比技術』における「堆積盆評価システム」の開発（その2）－石油の開発と備蓄 1991年8月

一覧に戻る